MD5 Rainbow Tables

From Computing and Software Wiki

(Difference between revisions)
Jump to: navigation, search
(→References)
Line 101: Line 101:
----
----
-
--[[User:Yuw7|Yuw7]] 22:30, 12 April 2009 (EDT)
+
--[[User:Yuw7|Yuw7]] 22:38, 12 April 2009 (EDT)

Revision as of 02:38, 13 April 2009

An example of a hash table containing only 1 character

A popular way of storing passwords for many websites, forums and other applications are through the use of MD5 hashing. When a user registers for a subscription and enters a password, that password is more than like passed through a MD5 hash function which outputs an encrypted key. This encrypted key is stored on a server, to keep a record of it for log in purposes. The next time the user tries to log in, they enter a password and this password is once again passed through the MD5 hash function and generates a temporary encrypted key. This temporary key is compared to the encrypted key that is previously stored and if they match then the server grants this user access. If the server is compromised, the attacker will only be able to retrieve a collection of hashed keys instead of the actual password of the users. However, through the use of MD5 rainbow tables, it allows the attacker to retrieve the original passwords as we shall see.

Contents

What is MD5?

Message-Digest 5 (MD5) hashing is an algorithm which converts a message into a 128-bit encrypted key, often called a hashed key. This hashing method works as a one way hash, meaning that original password is not retrievable from the hashed key alone. It has been implemented by many applications because it is a standard in RFC 1321. Recently, researchers have discovered that MD5 hashed keys were not collision proof. This means that two different passwords, when hashed together can result in the same hashed key.


What are Rainbow Tables?

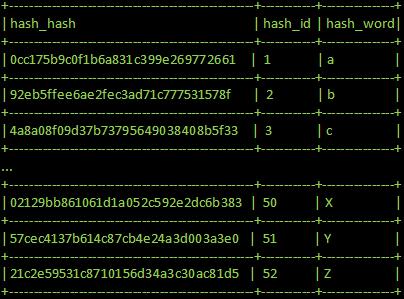
Rainbow tables are tables which contain a hashed key and the clear text message/password associated with the hashed key. This essentially makes a rainbow table a look up table, which allows an attacker to discover original passwords associated with a hashed key in a very short amount of time given that the rainbow table contains the hashed key. As one can guess, the more variations of hashed keys that are stored in a rainbow table, the more memory this table will require and the more time a computer would require to compile this table. This is known as the time-memory trade off.


How it works

Each time a cracker obtains a hashed key, they can try to retrieve the corresponding clear text message by getting a computer to brute-force attack the hashed key. However, for a message length of 7 characters, this may take hundreds of days; at which time, the message may no longer be relevant. MD5 hashing algorithm is particularly fast to calculate, normally in the order of milliseconds. However, when there are billions and billions of variations, the milliseconds quickly accumulate to days and months. So, by computing a large number of variations once and storing these values into a table, a user can just tell a computer to find a match for a particular hash key which eliminates the need to calculate any hashes. The only problem the user faces now is the amount of room required to store all this information. The principle of sacrificing memory for less computing time is called time-memory tradeoff, which will be explained in the later sections. If the hashed key is not found in the rainbow table, it means message rainbow table did not contain clear text message. This will force the attacker to either build a bigger rainbow table, brute-force it or give up.

Time-Memory Tradeoff

Time-memory trade off is the act of sacrificing memory in order to reduce computation time or vice-versa. For our particular application of rainbow tables, we can demonstrate this idea by the following example:
Assumptions*:

  1. One MD5 Hash entry in a rainbow table = 128 bits = 16 bytes, assuming that the clear-text associated with the hashed key is insgnificant.
  2. Each hash takes 10 milliseconds to compute.
  3. One character can have (26 uppercase letters) or (26 lowercase letters) or (10 numbers 0-9) = 62 choices

Various Rainbow Table Sizes with Associated Number of Characters
Number of Characters Total number of variations Total memory required Time required to compile table
1 62 992 bytes 6.2 millisecond
2 62x62 = 3,844 61504 bytes ~ 60 kb 384.4 millisecond
3 62^3 = 238,328 3.6 mb 23,832.8 millisecond = 23.83 seconds
4 62^4 = 14,776,336 225.5 mb 24.63 minutes
5 62^5 = 916,132,832 13.65 gb 25.45 hours
6 62^6 = 56,800,235,584 846.39 gb 65.74 days
6 62^7 = 35,216,114,606,208 51.25 tb 11.17 years



Explanation: In order for a rainbow table to store all the variations of 1 character with all the combination's, it would require 16 bytes x 62 = 992 bytes and a compile time of 62 x 0.1 millisecond = 6.2 millisecond.
If we increase it to 2 characters, it would be 62 choices for the first letter and 62 choices for the second letter, giving a total of 3844 different choices.
To store this combination, it would require 3844 * 16 bytes = 61504 bytes ~ 60 kilobytes and a compile time of 3844 x 0.1 millisecond = 384.4 millisecond
Continuing this trend to 7 characters, we get the last entry in the table.

Cost: With a terabyte of memory costing around 100 dollars in today's market, a rainbow table with all combination's up to 6 character can easily be stored.
However, if we increase the number of characters to just 1 more, we see that it will require 51.25 Terabytes. Costing about $5,200 in order to store the rainbow table. With 52 terabytes of information stored, it would still take a decent amount of time to search through each entry.

Conclusion: We can see from the table that as a rainbow table holds more variations, both the amount of room and compilation time increases exponentially.


[*]This is a very general scenario, most online applications allow special symbols such as @,# etc and even spaces. With a better processor, each hash would take less time to calculate, thus reducing table compilation time.

Solutions

Adding salt

Salt, in security, is the act of appending a number of bits (random or defined) to a password to increase its length. For every salt bit we add to the password, the number of raw brute-force attempts required increases by a factor of 2. So say we add 32 salt-bits to a password, it increases the attempts required to find the original password to (4,294,967,296) x (length of original password).

Using Variety

Many researchers agree that MD5 hashing algorithm is full of flaws and that it is not longer secure enough. So instead of using MD5, people can employ a different hashing algorithm such as MD6, SHA or wait for SHA-3 to be completed. As mentioned earlier, the time required for a rainbow table depends heavily on the hashing algorithm. So by choosing an algorithm that is slower than MD5, even a fast computer will take a long time to compile a table with a modest amount of variations.

Adding more items to the menu

For every symbol that a system allows a user to use, it increases the variations in a rainbow table by a factor. From the earlier example, it allowed each letter to have 62 different possibilities. If we were to allow a user to enter three more character, say ~, ! and @, we can calculate that for 7 letter words, there are 4,902,227,890,625 possibilities. Comparing this to the our example, we can see that by allowing an addition 3 symbols, it increases the variations by 500 billion different possibilities.

Frequently Changing the Order

By imposing a security policy which forces users to modify sensitive information, such as passwords, on a frequent basis, then there may be a chance that by the time an attacker finds a match in their rainbow table, the information that the attacker holds is no longer relevant. This is perhaps the easiest method, however it places more responsibility on the user's end.

Double the Serving

Another solution is to hash a hashed key. So when a user first enters a clear-text message, the server will hash the message to make the first hashed-key, then it will hash it again and store the final key. By doing this, the attacker must now have two rainbow tables in order to determine the original message. The first table would be a clear-text message with associated hashed key table, while the other table would be a table of hashed-keys with its associated hashes. A full rainbow table of hashed-keys with its associated hashes would required 16 ^ 32 entries. This calculation was derived by knowing that a hashed-key is 32 bits in length and each bit is represented in hexadecimal (16 variations).

Links

References

See Also

External Links

--Yuw7 22:38, 12 April 2009 (EDT)

Retrieved from "http://wiki.cas.mcmaster.ca/index.php/MD5_Rainbow_Tables"
Personal tools