Public Key Encryption Algorithms
From Computing and Software Wiki
(→References) |
(→How does Public Key Encryption work?) |
||
| (46 intermediate revisions not shown) | |||
| Line 1: | Line 1: | ||
| - | '''Public Key Encryption''' is also known as asymmetric cryptography | + | '''Public Key Encryption''' is also known as asymmetric cryptography. It is widely used in protecting information transmission through unsecured communication channel. The famous public key encryption algorithms include RSA, ECC and Rabin Cryptosystems. |
| + | |||
| + | |||
| Line 5: | Line 7: | ||
=== How does Public Key Encryption work? === | === How does Public Key Encryption work? === | ||
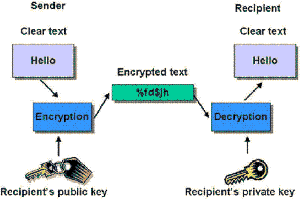
| - | The user has a pair of keys - public key and private key[ | + | The user has a pair of keys - public key and private key<sup>[http://en.wikipedia.org/wiki/Public-key_cryptography R1]</sup>. A message encrypted with a public key can only be decrypted by the corresponding private key. It is mathematically infeasible to derive private key from public key. |
| - | + | [[Image:pk_enc.gif|thumb|300px|center|A message encrypted with a public key can only be decrypted by the corresponding private key]] | |
===Advantage over Symmetric Encryption=== | ===Advantage over Symmetric Encryption=== | ||
| Line 16: | Line 18: | ||
===Digital signature to ensure authenticity=== | ===Digital signature to ensure authenticity=== | ||
| + | [[Image:digital_signature.jpg|thumb|300px|right|The sender encrypts a message with his own private key. The receiver decrypts the message using the sender’s public key]] | ||
The sender encrypts a message with his own private key. If the receiver can decrypt the sender’s message using the sender’s public key, this provides assurance that it is the sender (not a pretender) sent it<sup>[http://www.en.wikipedia.org/wiki/Public-key_cryptography R1]</sup>. | The sender encrypts a message with his own private key. If the receiver can decrypt the sender’s message using the sender’s public key, this provides assurance that it is the sender (not a pretender) sent it<sup>[http://www.en.wikipedia.org/wiki/Public-key_cryptography R1]</sup>. | ||
| - | |||
===Mathematical Theory=== | ===Mathematical Theory=== | ||
Many public key encryption algorithms are based on “Trap Door function”<sup>[http://www.krellinst.org/UCES/archive/modules/charlie/pke/node4.html R4]</sup>. Such type of function is easy to compute in one direction and difficult to calculate from the inverse direction. For example, f(x)=y is easy to compute y when x is given, but it is difficult to compute x when y is given. | Many public key encryption algorithms are based on “Trap Door function”<sup>[http://www.krellinst.org/UCES/archive/modules/charlie/pke/node4.html R4]</sup>. Such type of function is easy to compute in one direction and difficult to calculate from the inverse direction. For example, f(x)=y is easy to compute y when x is given, but it is difficult to compute x when y is given. | ||
| - | |||
== RSA == | == RSA == | ||
===What is RSA?=== | ===What is RSA?=== | ||
| - | RSA is a Public Key algorithm. The algorithm was publicly described in 1977 by Ron Rivest, Adi Shamir, and Leonard Adleman at MIT; the letters RSA are the initials of their surnames | + | RSA is a Public Key algorithm. The algorithm was publicly described in 1977 by Ron Rivest, Adi Shamir, and Leonard Adleman at MIT; the letters RSA are the initials of their surnames. It can be used to perform both signing and encryption. |
| - | + | ||
===Mathematical Theory=== | ===Mathematical Theory=== | ||
| Line 42: | Line 42: | ||
===A Working Example=== | ===A Working Example=== | ||
| - | + | [[Image:math_theory.gif|thumb|300px|right|The security of RSA is based on the difficulty of integer factorization]] | |
1. choose 2 prime numbers<sup>[http://www.di-mgt.com.au/rsa_alg.html R6]</sup> : | 1. choose 2 prime numbers<sup>[http://www.di-mgt.com.au/rsa_alg.html R6]</sup> : | ||
| Line 74: | Line 74: | ||
Decrypted message M’ = C^D mod N = 13^7 mod 33 = 7 | Decrypted message M’ = C^D mod N = 13^7 mod 33 = 7 | ||
| - | |||
| Line 92: | Line 91: | ||
The discrete logarithm problem on such elliptic curve groups is so difficult. Thus keys in elliptic curve cryptography can be chosen to be much shorter for a comparable level of security. | The discrete logarithm problem on such elliptic curve groups is so difficult. Thus keys in elliptic curve cryptography can be chosen to be much shorter for a comparable level of security. | ||
| + | |||
| Line 103: | Line 103: | ||
== Rabin cryptosystem == | == Rabin cryptosystem == | ||
| - | '''Rabin Cyptosystem''' | + | '''Rabin Cyptosystem''' |
| + | |||
| + | In 1979, Rabin invented the Rabin cryptosystem, the first asymmetric cryptosystem whose security was proved equivalent to the intractability of integer factorization<sup>[R10]</sup>. | ||
For encryption, Rabin Cyptosystem is more efficient than RSA. For decryption, the efficiency of Rabin Cyptosystem is same as RSA. | For encryption, Rabin Cyptosystem is more efficient than RSA. For decryption, the efficiency of Rabin Cyptosystem is same as RSA. | ||
| Line 129: | Line 131: | ||
[R9] Microsoft Help and Support. "Description of Symmetric and Asymmetric Encryption". Retrieved on 2008-04-05. http://support.microsoft.com/kb/246071 | [R9] Microsoft Help and Support. "Description of Symmetric and Asymmetric Encryption". Retrieved on 2008-04-05. http://support.microsoft.com/kb/246071 | ||
| + | |||
| + | [R10] Rabin, MO (January 1979). "Digital signatures and public-key functions as intractable as factorization". {MIT Laboratory of Computer Science Technical Report.} | ||
| + | |||
== See Also == | == See Also == | ||
| Line 135: | Line 140: | ||
[[Conventional Encryption Algorithms]]<BR> | [[Conventional Encryption Algorithms]]<BR> | ||
[[Digital Identity]]<BR> | [[Digital Identity]]<BR> | ||
| + | |||
== External Links == | == External Links == | ||
| + | * [http://www.rsa.com/ RSA company] | ||
| + | * [http://www.certicom.com/index.php?action=ecc,res_home Certicom] | ||
| + | * [http://www.seas.harvard.edu/directory/professionalbio/index.html?id=2542u Dr. Rabin] | ||
| + | |||
| + | |||
| + | --[[User:Zhaoy36|Zhaoy36]] 17:09, 5 April 2008 (EDT) | ||
Current revision as of 22:34, 12 April 2008
Public Key Encryption is also known as asymmetric cryptography. It is widely used in protecting information transmission through unsecured communication channel. The famous public key encryption algorithms include RSA, ECC and Rabin Cryptosystems.
Contents |
Public Key Encryption
How does Public Key Encryption work?
The user has a pair of keys - public key and private keyR1. A message encrypted with a public key can only be decrypted by the corresponding private key. It is mathematically infeasible to derive private key from public key.
Advantage over Symmetric Encryption
Symmetric cryptography uses one key for both encryption and decryption. When the key is distributes to the sender and receiver, key may be leaked in the way.
Asymmetric encryption can protect information transmission through unsecured communication channel. Because it is mathematically infeasible to derive private key from public key, public key can be exposed to outside world. This prevents a third party from copying a key while it is in the way and further spying on the communication between sender and receiverR9.
Digital signature to ensure authenticity
The sender encrypts a message with his own private key. If the receiver can decrypt the sender’s message using the sender’s public key, this provides assurance that it is the sender (not a pretender) sent itR1.
Mathematical Theory
Many public key encryption algorithms are based on “Trap Door function”R4. Such type of function is easy to compute in one direction and difficult to calculate from the inverse direction. For example, f(x)=y is easy to compute y when x is given, but it is difficult to compute x when y is given.
RSA
What is RSA?
RSA is a Public Key algorithm. The algorithm was publicly described in 1977 by Ron Rivest, Adi Shamir, and Leonard Adleman at MIT; the letters RSA are the initials of their surnames. It can be used to perform both signing and encryption.
Mathematical Theory
The security of RSA is based on the difficulty of integer factorization: Finding large primes and multiplying them together is easy. However, from the product to find the factors is hard. There is no known efficient general technique to solve this problem. However, due to recent progress in factoring integers, RSA public keys are recommended to be at least 1024 bits long to provide adequate security.
Speed
RSA is much slower than symmetric cryptosystems.
A Working Example
1. choose 2 prime numbersR6 :
P=11, Q=3
2. compute N=P*Q:
N=11*3=33
3. compute L=(P-1)*(Q-1):
L= (11-1)*(3-1) = 10*2=20
4. choose E>1 and coprime to L:
Choose E=3
5. compute D such that E*D = 1 mod L:
D = 7 such that D*E =7*3 = 21 = 1 mod 20
6. public key is (N, E), private key is (N, D):
PK = (33, 3), SK= (33, 7)
7. Encrypt message using PK with C = M^E mod N:
Assume a message M=7, cipher text C = M^E mod N = 7^3 mod 33 = 343 mod 33 =13
8. Decrypt cipher text using SK with M' = C^D mod N:
Decrypted message M’ = C^D mod N = 13^7 mod 33 = 7
Elliptic curve cryptography
What is ECC?
Elliptic curve cryptography (ECC) is a public-key algorithm based on the algebraic structure of elliptic curves over finite fieldsR7.
Mathematical Theory
The security of Elliptic curve cryptography is based on the difficulty of solving discrete logarithm problem.
An elliptic curve has the following form:
y^2=x^3+ax+b.
The discrete logarithm problem on such elliptic curve groups is so difficult. Thus keys in elliptic curve cryptography can be chosen to be much shorter for a comparable level of security.
Efficiency
Elliptic curves cryptography is more efficient with respect to key size.
Comparing with other public key algorithmsR7, if the user wants 128-bit security, he needs a curve to create 256-bit key. However, if the user chooses DSA, it would require 3072-bit public keys and 256-bit private keys. For RSA, it would require 3072-bit public and private keys.
Rabin cryptosystem
Rabin Cyptosystem
In 1979, Rabin invented the Rabin cryptosystem, the first asymmetric cryptosystem whose security was proved equivalent to the intractability of integer factorization[R10].
For encryption, Rabin Cyptosystem is more efficient than RSA. For decryption, the efficiency of Rabin Cyptosystem is same as RSA.
Rabin system is more secure than RSA.
References
[R1] Wikipedia. "Public-key cryptography", Wikipedia, 2008-04-02. Retrieved on 2008-04-02. http://en.wikipedia.org/wiki/Public-key_cryptography
[R2] Applied Cryptography, 2nd Ed, Bruce Schneier. ISBN: 0-471-11709-9 Publisher: Wiley
[R3] Anoop MS (2007). Public key Cryptography - Applications Algorithms and Mathematical Explanations
[R4] Charlie Fletcher. "Public Key Encryption". Retrieved on 2008-04-02. http://www.krellinst.org/UCES/archive/modules/charlie/pke/node4.html
[R5] Wikipedia. "RSA", Wikipedia. Retrieved on 2008-04-02. http://en.wikipedia.org/wiki/RSA
[R6] DI Management, "RSA Algorithm", Retrieved on 2008-04-02. http://www.di-mgt.com.au/rsa_alg.html
[R7] Wikipedia. "Elliptic curve cryptography", Wikipedia. Retrieved on 2008-04-02. http://en.wikipedia.org/wiki/Elliptic_curve_cryptography
[R8] Wikipedia. "Rabin cryptosystem", Wikipedia. Retrieved on 2008-04-02. http://en.wikipedia.org/wiki/Rabin_cryptosystem
[R9] Microsoft Help and Support. "Description of Symmetric and Asymmetric Encryption". Retrieved on 2008-04-05. http://support.microsoft.com/kb/246071
[R10] Rabin, MO (January 1979). "Digital signatures and public-key functions as intractable as factorization". {MIT Laboratory of Computer Science Technical Report.}
See Also
Blowfish
Digital Signatures
Conventional Encryption Algorithms
Digital Identity
External Links
--Zhaoy36 17:09, 5 April 2008 (EDT)