Conventional Encryption Algorithms
From Computing and Software Wiki
(→Popular Algorithms) |
|||
| (30 intermediate revisions not shown) | |||
| Line 1: | Line 1: | ||
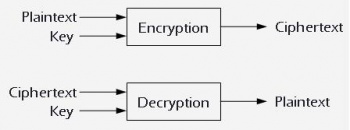
| - | '''Conventional Encryption''' | + | '''Conventional Encryption''' involves transforming plaintext messages into ciphertext messages that are to be decrypted only by the intended receiver. Both sender and receiver agree upon a secrete key to be used in encrypting and decrypting. Usually the secrete key is transmitted via public key encryption methods. |
| - | [[Image:FlowDiagram.jpg|thumb|350px| | + | |
| + | [[Image:FlowDiagram.jpg|thumb|350px|centre|Figure 1: Flow Diagram]] | ||
| + | |||
| + | In conventional encryption, it is assumed that it is mathematically impossible to derive the plaintext from the ciphertext without the key.<sup>[R1]</sup> Therefore, it is essential that the key remains secret. | ||
| + | |||
| + | These encryption algorithms are used in practice due to their efficiency in encrypting/decrypting but these algorithms have vulnerabilities. One aspect of these vulnerabilities is the total number of keys available to choose from. Larger key domains reduce possibility of brute force attacks. The key length is another aspect of these vulnerabilities since they will produce periodic patterns in the ciphertext. Longer keys often reduce periodicity. The goal of conventional encryption algorithms is to produce truly randomized ciphertexts, such that the use of frequency analysis on individual ciphertext symbols or ciphertext blocks is useless. | ||
__TOC__ | __TOC__ | ||
| Line 9: | Line 14: | ||
=== Monoalphabetic === | === Monoalphabetic === | ||
| - | This is a substitution technique that uses a single alphabet to replace symbols of plaintext for symbols of ciphertext as dictated by the key. The key often represents the number of symbols to shift the plaintext from a circular alphabet. These techniques are relatively easy to break due to the fact that symbol frequencies remain invariant. | + | This is a substitution technique that uses a single alphabet to replace symbols of plaintext for symbols of ciphertext as dictated by the key. The key often represents the number of symbols to shift the plaintext from a circular alphabet. These techniques are relatively easy to break due to the fact that symbol frequencies remain invariant.<sup>[R5]</sup> |
=== Polyalphabetic === | === Polyalphabetic === | ||
| Line 15: | Line 20: | ||
=== Polygraphic === | === Polygraphic === | ||
| - | This is a substitution technique that replaces a group of n plaintext symbols by a group of ''n'' ciphertext symbols. In doing so, the individual frequency of symbols is hidden. In generality, this technique is similar to that of monoalphabetic ciphers with only using larger alphabets. | + | This is a substitution technique that replaces a group of n plaintext symbols by a group of ''n'' ciphertext symbols.<sup>[R2]</sup> In doing so, the individual frequency of symbols is hidden. In generality, this technique is similar to that of monoalphabetic ciphers with only using larger alphabets. |
=== Route Transposition === | === Route Transposition === | ||
| - | This is a transposition technique where the plaintext is first written out in an ''mxn'' grid region. The key often represents a path on how to read from the grid, such as clockwise outward spiral, vertical zigzag, triangulation, etc. The ciphertext then becomes the sequence of symbols as read by the path. These techniques provide enormous amounts of available keys in which to use. However, some choices of keys are poor ones since they may leave sections of the ciphertext in their original or reversed plaintext order giving hints as to which key where used. | + | This is a transposition technique where the plaintext is first written out in an ''mxn'' grid region. The key often represents a path on how to read from the grid, such as clockwise outward spiral, vertical zigzag, triangulation, etc.<sup>[R3]</sup> The ciphertext then becomes the sequence of symbols as read by the path. These techniques provide enormous amounts of available keys in which to use. However, some choices of keys are poor ones since they may leave sections of the ciphertext in their original or reversed plaintext order giving hints as to which key where used. |
=== Columnar Transposition === | === Columnar Transposition === | ||
| Line 24: | Line 29: | ||
=== Synchronous Stream === | === Synchronous Stream === | ||
| - | This is a stream translation technique that combines plaintext with a key stream usually in the form of an XOR operation to form ciphertext one symbol at a time. These techniques require that the encoder and decoder be synchronized in the information they are processing. If information get introduced or lost during transition, decryption will be erroneous. If information gets corrupted only the particular symbol remains corrupted. | + | This is a stream translation technique that combines plaintext with a key stream usually in the form of an XOR operation to form ciphertext one symbol at a time.<sup>[R4]</sup> These techniques require that the encoder and decoder be synchronized in the information they are processing. If information get introduced or lost during transition, decryption will be erroneous. If information gets corrupted only the particular symbol remains corrupted. |
=== Asynchronous Stream === | === Asynchronous Stream === | ||
| Line 30: | Line 35: | ||
=== Iterated Block === | === Iterated Block === | ||
| - | This is a block translation technique that iteratively converts an n-sized block of plaintext into ciphertext at the same time. | + | This is a block translation technique that iteratively converts an ''n''-sized block of plaintext into ciphertext at the same time. |
=== Fractioned Block === | === Fractioned Block === | ||
| Line 49: | Line 54: | ||
|- | |- | ||
| [http://en.wikipedia.org/wiki/ROT13 ROT13] || Monoalphabetic | | [http://en.wikipedia.org/wiki/ROT13 ROT13] || Monoalphabetic | ||
| + | |- | ||
| + | | [http://en.wikipedia.org/wiki/Four-square_cipher Four Square] || Monoalphabetic | ||
|- | |- | ||
| [http://en.wikipedia.org/wiki/Running_key_cipher Running Key] || Polyalphabetic | | [http://en.wikipedia.org/wiki/Running_key_cipher Running Key] || Polyalphabetic | ||
| Line 57: | Line 64: | ||
|- | |- | ||
| [http://en.wikipedia.org/wiki/Playfair_cipher Playfair] || Polygraphic | | [http://en.wikipedia.org/wiki/Playfair_cipher Playfair] || Polygraphic | ||
| + | |- | ||
| + | | [http://en.wikipedia.org/wiki/Trifid_cipher Trifid] || Polygraphic | ||
|- | |- | ||
| [http://en.wikipedia.org/wiki/Rail_Fence_Cipher Rail Fence] || Route Transposition | | [http://en.wikipedia.org/wiki/Rail_Fence_Cipher Rail Fence] || Route Transposition | ||
|- | |- | ||
| [http://en.wikipedia.org/wiki/A5/1 A5/1] || Synchronous Stream | | [http://en.wikipedia.org/wiki/A5/1 A5/1] || Synchronous Stream | ||
| + | |- | ||
| + | | [http://en.wikipedia.org/wiki/Rabbit_%28cipher%29 Rabbit] || Asynchronous Stream | ||
|- | |- | ||
| [http://en.wikipedia.org/wiki/Autokey_cipher Autokey] || Asynchronous Stream | | [http://en.wikipedia.org/wiki/Autokey_cipher Autokey] || Asynchronous Stream | ||
| Line 76: | Line 87: | ||
| [http://en.wikipedia.org/wiki/ADFGVX_cipher ADFGVX] || Fractionated Block | | [http://en.wikipedia.org/wiki/ADFGVX_cipher ADFGVX] || Fractionated Block | ||
|- | |- | ||
| - | | [] || | + | | [http://en.wikipedia.org/wiki/Straddling_checkerboard Straddling Checkboard] || Fractionated Block |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
|- | |- | ||
| [http://en.wikipedia.org/wiki/Bacon%27s_cipher Bacon] || Steganographic | | [http://en.wikipedia.org/wiki/Bacon%27s_cipher Bacon] || Steganographic | ||
| Line 90: | Line 93: | ||
== References == | == References == | ||
| - | [ | + | [R1] McMaster University - CAS. "Overview of Cryptography". Software Engineering 4C03, Lecture 07. 2008 |
| - | [ | + | |
| + | [R2] Irwin, Paul L. "Elementary Cryptanalysis - A Mathematical Approach". Copyright Yale University. 1966 | ||
| + | |||
| + | [R3] Foster, Caxton C. "Cryptanalysis For Microcomputers". University of Massachusetts. 1982 | ||
| + | |||
| + | [R4] Wikipedia. "Stream Cipher", Wikipedia, 2008-02-02. Retrieved on April 9/2008. http://en.wikipedia.org/wiki/Stream_cipher | ||
| + | |||
| + | [R5] Beker H., Piper F. "Cypher Systems". Northwood Publications. 1982 | ||
== See Also == | == See Also == | ||
| Line 100: | Line 110: | ||
== External Links == | == External Links == | ||
[http://www.ling.ohio-state.edu/~cbrew/2008/winter/484/monoalphabetic.pdf Monoalphabetic Ciphers] | [http://www.ling.ohio-state.edu/~cbrew/2008/winter/484/monoalphabetic.pdf Monoalphabetic Ciphers] | ||
| + | |||
| + | [http://www.quadibloc.com/crypto/pp010303.htm Polyalphabetic Substitution] | ||
| + | |||
| + | [http://www.quadibloc.com/crypto/pp010302.htm Polygraphic Ciphers & Fractionation] | ||
| + | |||
| + | [http://www.mathsyear2000.org/explorer/codebreaking/transposition-ciphers.php Codebreaking] | ||
| - | [[User:Angiusei| | + | --[[User:Angiusei|Angiusei]] 17:03, 10 July 2008 (EDT) |
Current revision as of 21:03, 10 July 2008
Conventional Encryption involves transforming plaintext messages into ciphertext messages that are to be decrypted only by the intended receiver. Both sender and receiver agree upon a secrete key to be used in encrypting and decrypting. Usually the secrete key is transmitted via public key encryption methods.
In conventional encryption, it is assumed that it is mathematically impossible to derive the plaintext from the ciphertext without the key.[R1] Therefore, it is essential that the key remains secret.
These encryption algorithms are used in practice due to their efficiency in encrypting/decrypting but these algorithms have vulnerabilities. One aspect of these vulnerabilities is the total number of keys available to choose from. Larger key domains reduce possibility of brute force attacks. The key length is another aspect of these vulnerabilities since they will produce periodic patterns in the ciphertext. Longer keys often reduce periodicity. The goal of conventional encryption algorithms is to produce truly randomized ciphertexts, such that the use of frequency analysis on individual ciphertext symbols or ciphertext blocks is useless.
Contents |
Classification of Ciphers
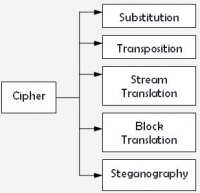
There are several techniques in which encryption algorithms can produce ciphertext. The simplest forms of encryption are via substitution, where plaintext symbols are replaced and via transposition, where plaintext symbols are rearranged. Other approaches such as stream and block translation involve converting plaintext to ciphertext either one symbol at a time or several symbols at a time respectively. In addition, steganographic techniques can be used, where symbols are introduced in the ciphertext to hide the plaintext meaning. A particular encryption/decryption implementation could incorporate multiple techniques to increase security.
Monoalphabetic
This is a substitution technique that uses a single alphabet to replace symbols of plaintext for symbols of ciphertext as dictated by the key. The key often represents the number of symbols to shift the plaintext from a circular alphabet. These techniques are relatively easy to break due to the fact that symbol frequencies remain invariant.[R5]
Polyalphabetic
This is a substitution technique that uses multiple alphabets to replace symbols of plaintext for symbols of ciphertext as dictated by the key. The key often represents a keyword where each letter defines the alphabet being used to encrypt each symbol of the plaintext. The keyword is repeated throughout the length of the message. These techniques suppress individual symbol frequency making these ciphers harder to break. However, the keyword length determines the periodicity in which alphabets are used. This periodicity is a major vulnerability of these types of ciphers.
Polygraphic
This is a substitution technique that replaces a group of n plaintext symbols by a group of n ciphertext symbols.[R2] In doing so, the individual frequency of symbols is hidden. In generality, this technique is similar to that of monoalphabetic ciphers with only using larger alphabets.
Route Transposition
This is a transposition technique where the plaintext is first written out in an mxn grid region. The key often represents a path on how to read from the grid, such as clockwise outward spiral, vertical zigzag, triangulation, etc.[R3] The ciphertext then becomes the sequence of symbols as read by the path. These techniques provide enormous amounts of available keys in which to use. However, some choices of keys are poor ones since they may leave sections of the ciphertext in their original or reversed plaintext order giving hints as to which key where used.
Columnar Transposition
This is a transposition technique where the plaintext is first written out in n-length rows. The key often represents a keyword of length n that defines the plaintext ordering of columns. The ordering could be done by sorting the keyword letters in alphabetical order or in any predefined order.
Synchronous Stream
This is a stream translation technique that combines plaintext with a key stream usually in the form of an XOR operation to form ciphertext one symbol at a time.[R4] These techniques require that the encoder and decoder be synchronized in the information they are processing. If information get introduced or lost during transition, decryption will be erroneous. If information gets corrupted only the particular symbol remains corrupted.
Asynchronous Stream
This is a stream translation technique that combines plaintext with a key stream that is generated from some fixed number of ciphertext symbols to produce the next ciphertext symbol.
Iterated Block
This is a block translation technique that iteratively converts an n-sized block of plaintext into ciphertext at the same time.
Fractioned Block
This is a block translation technique that breaks up single symbols into parts and then combines the pieces of multiple plaintext letters in order to get the ciphertext.
Steganographic
This is a technique that involves inserting random symbols at random locations of a plaintext message with the goal of hiding the message.
Popular Algorithms
| Algorithm | Type |
|---|---|
| Caesar | Monoalphabetic |
| ROT13 | Monoalphabetic |
| Four Square | Monoalphabetic |
| Running Key | Polyalphabetic |
| Vigenère | Polyalphabetic |
| One Time Pad | Polyalphabetic |
| Playfair | Polygraphic |
| Trifid | Polygraphic |
| Rail Fence | Route Transposition |
| A5/1 | Synchronous Stream |
| Rabbit | Asynchronous Stream |
| Autokey | Asynchronous Stream |
| AES | Iterated Block |
| Blowfish | Iterated Block |
| DES | Iterated Block |
| IDEA | Iterated Block |
| SMS4 | Iterated Block |
| ADFGVX | Fractionated Block |
| Straddling Checkboard | Fractionated Block |
| Bacon | Steganographic |
References
[R1] McMaster University - CAS. "Overview of Cryptography". Software Engineering 4C03, Lecture 07. 2008
[R2] Irwin, Paul L. "Elementary Cryptanalysis - A Mathematical Approach". Copyright Yale University. 1966
[R3] Foster, Caxton C. "Cryptanalysis For Microcomputers". University of Massachusetts. 1982
[R4] Wikipedia. "Stream Cipher", Wikipedia, 2008-02-02. Retrieved on April 9/2008. http://en.wikipedia.org/wiki/Stream_cipher
[R5] Beker H., Piper F. "Cypher Systems". Northwood Publications. 1982
See Also
Public Key Encryption Algorithms
External Links
Polygraphic Ciphers & Fractionation
--Angiusei 17:03, 10 July 2008 (EDT)